(해결 코드는 맨 아래 있으므로, 맨 아래를 참고)
평소 두 인자 a, b를 받고 a의 b제곱을 구하라 하면
간단하게 Math.pow() 메서드를 이용하거나, 다음과 같이 구현했을 것이다.
class Solution {
public long power(int base, int exponent) {
if (exponent == 0) return 1;
if (exponent == 1) return base;
for (int i = 1; i < exponent; i++) {
base *= base;
}
return base;
}
}
이 코드의 경우, 시간 복잡도는 Big-O 기준 O(n)이다.
좀 더 효율적으로 코드를 짜본다면, O(logN)까지 줄일 수 있다고 한다.
바로 분할 정복과 모듈러 곱셈 역원(Modular Inverse)을 이용하는 것이다.
분할 정복은 간략하게 다음과 같이 설명될 수 있을 것 같다.

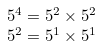
5의 16제곱은 5의 8제곱 두 개의 곱으로 나타낼 수 있겠고,
5의 8제곱은 5의 4제곱 두 개의 곱으로 나타낼 수 있는, 이런 과정이 반복되는 걸 말한다.
모듈러 곱셈 역원은
5 mod 3과 8 mod 3은 서로 같다.
즉, 5 % 3과 8 % 3의 값은 서로 같다는 걸 뜻하는 것 같다.
(아래 코드에서는 % 94906249는 코드 동작이 int의 범위 내에서 작동하도록 해주는 것이지만,
이 모듈러 곱셈 역원을 이용한다는 말인 것 같다.)
분할 정복과 모듈러 곱셈 역원을 이용한 알고리즘 문제를 푼 코드는 다음과 같다.
문제 : 두 수를 입력받아 거듭제곱을 리턴해야 합니다.
출력 :
- long 타입을 리턴해야 합니다.
- 실제 계산 결과를 94,906,249로 나눈 나머지를 리턴해야 합니다.
주의 사항 :
- Math.pow, 거듭제곱 연산자 사용은 금지됩니다.
- 시간복잡도 O(logN)을 만족해야 합니다.
- 나머지를 구하는 이유는 계산 결과가 컴퓨터로 나타낼 수 있는 수의 범위를 넘을 수 있기 때문입니다. 하지만 모든 연산이 끝난 뒤에 그 결과를 94,906,249로 나누려고 해서는 안 됩니다. 연산 중간에도 이 범위를 넘을 수 있기 때문에, 연산을 할 때마다 나머지를 구하고 그 결과에 연산을 이어가시기 바랍니다.
< 해결 코드 >
public class Solution {
public long power(int base, int exponent) {
// 지수가 0인 경우(종료 조건)
if (exponent == 0) return 1;
// 반으로 나눈 거듭제곱 계산
long tmp = power(base, exponent / 2);
long result = tmp * tmp % 94_906_249;
// 지수가 짝수인 경우
if (exponent % 2 == 0) return result;
// 지수가 홀수인 경우
else return base * result % 94_906_249;
}
}
'Develop > Algorithm' 카테고리의 다른 글
| treeBFS - 깊이 우선 탐색 알고리즘 (0) | 2022.10.26 |
|---|---|
| treeDFS - 깊이 우선 탐색 알고리즘 (0) | 2022.10.25 |
| 소수 알고리즘 - 제곱근 & 에라토스테네스의 체 이용 (0) | 2022.10.23 |
| a를 b로 나눈 수를 올림할 때, (0) | 2022.10.23 |
| Java) 버블 정렬(Bubble Sort) 알고리즘 (0) | 2022.10.20 |


