조합은 n 개의 숫자 중에서 r 개의 수를 순서 없이 뽑는 경우를 의미한다.
- https://ko.wikipedia.org/wiki/%EC%A1%B0%ED%95%A9
조합은 기호로 다음과 같이 나타낼 수 있다.
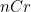

** 조합은 하나의 원소를 선택할 경우 + 하나의 원소를 선택하지 않을 경우
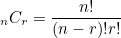
* n개 중에 m개를 뽑는 경우의 수를 구하는 신기한 풀이 (이해 필요) *
class Test {
public long solution(int N, int M) {
M = Math.min(N - M, M);
if (M == 0)
return 1;
long answer = solution(N - 1, M - 1);
answer *= N;
answer /= M;
return answer;
}
}
// 순열과 조합의 공식을 재귀로 만든 코드
// 조합 = 순열 / share!로 표현할 수도 있어서 재귀적으로 balls를 하나씩 줄여가면서 순열을 share 팩토리얼로 나눠줌
// nCr과 nCn-r이 같은 것을 이용해서 순회 횟수를 줄이는 것도 해준 것
조합 경우의 수 구하기
public int combination(int n, int r) {
if(n == r || r == 0) return 1;
else return combination(n - 1, r - 1) + combination(n - 1, r);
}
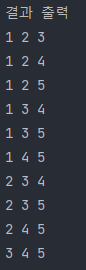
뽑힌 조합들을 구하기
1. 백트래킹 이용
public class Test {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5}; // 조합을 만들 배열
int r = 3; // 뽑을 숫자 개수
boolean[] visited = new boolean[arr.length];
combination(arr, visited, 0, r);
}
// 백트래킹을 이용해 구현
static void combination(int[] arr, boolean[] visited, int start, int r) {
if (r == 0) {
print(arr, visited);
return;
} else {
for (int i = start; i < arr.length; i++) {
visited[i] = true;
combination(arr, visited, i + 1, r - 1);
visited[i] = false;
}
}
}
// 배열 출력
static void print(int[] arr, boolean[] visited) {
for(int i = 0; i < arr.length; i++) {
if(visited[i] == true)
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
2. 재귀 이용
public class Test {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5}; // 조합을 만들 배열
int r = 3; // 뽑을 숫자 개수
boolean[] visited = new boolean[arr.length];
combination(arr, visited, 0, r);
}
// 재귀 이용 구현
static void combination(int[] arr, boolean[] visited, int depth, int r) {
if(r == 0) {
print(arr, visited);
return;
}
if(depth == arr.length) {
return;
} else {
visited[depth] = true;
combination(arr, visited, depth + 1, r - 1);
visited[depth] = false;
combination(arr, visited, depth + 1, r);
}
}
// 배열 출력
static void print(int[] arr, boolean[] visited) {
for(int i = 0; i < arr.length; i++) {
if(visited[i] == true)
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
- Ref)
- https://minhamina.tistory.com/38
- https://limkydev.tistory.com/178 [Java] 조합, 중복 조합, 순열, 중복순열 소스
'Develop > Algorithm' 카테고리의 다른 글
| 모듈러 연산(Modulo Operation) (0) | 2022.12.24 |
|---|---|
| 연속된 수의 합으로 특정 수를 만들 수 있는 경우의 수 (0) | 2022.12.21 |
| 약수 개수 알고리즘 (0) | 2022.11.18 |
| 유클리드 호제법을 이용한 최소공배수, 최대공약수 (0) | 2022.11.05 |
| 이진 탐색(Binary Search) (0) | 2022.11.01 |

